MOSFET噪声特性的标定与五管OTA的噪声优化
实验一:MOSFET噪声特性的标定¶
一、实验目标¶
- 学会利用NOISE仿真工具。
- 通过仿真查看PMOS晶体管的热噪声和闪烁噪声,理解并估算折射频率。
- 通过仿真得到本课程所用工艺的热噪声系数\(\gamma\)和闪烁噪声系数\(K_{F}\)。
二、实验要求¶
- 仿真推算出PMOS的热噪声系数、闪烁噪声系数以及频率系数
- 对比讨论PMOS和NMOS品体管在作为低噪声差分对时哪个更适合。
三、实验步骤¶
1.电路绘制与静态工作点的确定¶
图1:NOISE仿真电路
- 这里用来计算PMOS的噪声特性,为了方便与教材中测得的NMOS对比,这里直接采用与教材相同的电压参数~(不是我懒)~
2. 设置NOISE仿真¶
- 为了获得更精确的结果,将AC仿真点数设置为50/dec,且NOISE仿真间隔数量也为50。参数设置如下:
图2:NOISE仿真设置
3.转折频率¶
- 对比各频率下的NOISE仿真结果可以推断出,PMOS晶体管PM0的转折频率在200kHz和250kHz之间,如下图所示:
图3:PMOS晶体管在100kHz和1MHZ下的NOISE仿真结果
4.晶体管热噪声参数计算¶
- 首先,op仿真的PMOS参数如下
图4:PMOS晶体管在op仿真结果参数
- AC仿真得到增益\(A_0\)=50.5
图5:PMOS晶体管输入到输出的放大系数A0
- MOSFET等效输入热噪声
仿真结果给出的是输出噪声,因此要对其进行等效转换,即除以输入到输出的放大系数\(A_0\)。
5.晶体管闪烁噪声计算¶
- 在拉扎维教材中得到:
- 第一,因为在大多数应用中遇到的信号不包含非常低频的成分,所以我们的观察窗不必很长。例如,声音信号低于20Hz频率的能量可以忽略,并且如果一个噪声成分变化得非常慢,它就不会显著损坏声音。
-
第二,闪烁噪声功率对\(f_L\)的对数关系允许在选择\(f_L\)时有一定的误差容限。
-
所以,对于式子\(\overline{V^2_{n,1/f,N}}=\frac{k_{F,N}}{C_{ox}WL}(\frac{1}{f})^{\alpha_{N}}\)拟合\({\alpha_{N}}\)时,选择从500Hz的频率开始。
-
通过前述仿真可以得到闪烁噪声功率在不同频率下的值,记录如下:
| 频率(\(Hz\)) | 闪烁噪声功率(\(v^2/Hz\)) |
|---|---|
| 500 | 1.0228n |
| 1k | 468.3505p |
| 1.5849k | 278.2473p |
| 2.5119k | 165.3069p |
| 7.9433k | 44.9719p |
| 10.0000k | 34.6634p |
| 25.1189k | 12.2346p |
| 50.1187k | 5.6025p |
| 100.0000k | 2.5655p |
| 158.4893k | 1.5241p |
| 501.1872k | 414.5739f |
| 794.3282k | 246.2309f |
| 1000.0000k | 189.7389f |
表1:不同频率下的闪烁噪声功率
- 对闪烁噪声功率\(f_n\)和频率\(f\)取对数后作一元线性拟合,可得到拟合的直线斜率的相反数即为\({\alpha_{N}}\)。结果如下
图6:lgfn与lgf的拟合图
-
可得 $$ \alpha_{N}=1.13 $$
-
此时可计算得到PMOS晶体管的闪烁噪声系数\(K_{F,N}\)。同样需要注意的是,仿真结果给出的是输出噪声,系数的计算仍旧需要对其进行等效转换:
与拉扎维教材上的数量级一致。
四、实验总结与思考¶
- 转折频率:仿真结果显示PMOS的转折频率在200kHz和250kHz之间。
- 热噪声系数:通过仿真结果并结合增益对输出噪声进行等效转换,得到了PMOS晶体管的热噪声系数\(\gamma_{p}\approx0.75\)。
- 闪烁噪声系数:记录了各频率下的闪烁噪声功率数据,通过对频率和噪声功率的对数拟合,计算出闪烁噪声系数\(K_{F,N}=7.75*10^{-25}V^2F\)。
- 噪声特性对比 :
-
热噪声:PMOS晶体管由于载流子迁移率较低,通常会产生较低的热噪声,而NMOS具有较高的迁移率,热噪声相对较大。对于低频应用中,PMOS在热噪声方面更具优势。
-
闪烁噪声(1/f噪声):在低频同等条件下,将PMOS的闪烁噪声功率与NMOS(在教材192页)做对比。PMOS的闪烁噪声比NMOS更小,尤其在低频时,闪烁噪声对信号影响显著。因此在低频差分放大电路中,PMOS作为低噪声输入对的优势更明显。
- 综上,PMOS晶体管在作为低噪声差分对时更具优势,特别是在低频应用中能更好地抑制热噪声和闪烁噪声的干扰,提升信噪比。
- 本实验帮助学会利用NOISE仿真工具,同时加深了对MOSFET噪声特性的理解,尤其是热噪声和闪烁噪声在电路设计中所起的作用,为低噪声电路设计提供了参考依据。
实验二:五管OTA的噪声优化¶
一、实验目标¶
- 掌握基本单元(电流镜、差分对等)的等效噪声计算。
- 了解电路中的噪声情况,并掌握噪声优化的方法。
- 通过仿真分析热噪声和闪烁噪声的在低频与高频时的特点。
二、实验要求¶
- 在“10.2.2仿真实验:五管OTA的噪声优化”的基础上,通过优化晶体管尺寸,使得总等效输入噪声小于10\(uV_{RMS}\)。
- 通过计算分析其中热噪声和闪烁噪声的占比。
三、实验步骤¶
1.优化尺寸¶
- 考虑到
可以看到本征增益\(A_{0}\)的增加可以显著降低等效输入噪声,并且五管OTA的增益可以达到k级别,而\({\overline{V_{n,1/f,N}}}\)通常只有m级别,这样一除,数量级就可以可以达到\(10^{-6}\),可以轻松满足要求,
-
因此现在目标就变为增大五管OTA的增益即可。
-
考虑到五管OTA的增益
在本电路中,静态电流被电流源钳制,所以跨导很难有大的突破。可以对\(r_o\)入手,增大管子宽长比,降低沟道长度调制效应。
- 由于之前的计算公式错误,导致迭代了很多次误以为没有达到要求但实际上早已满足指标。本次实验的迭代的中间过程数据没有意义,
主要是也丢失了。直接给出最终的电路参数如下
图7:优化后的电路图
- AC仿真如下,增益\(A_{0}\)=779,0db点约为12Mhz。
图8:AC仿真
- 噪声仿真的一组数据如下,鉴于0db点为12MHz,之后的频率意义不大,所以在AC仿真的频率只从1Hz到12MHz
图9:噪声仿真
- 于是有:
2.分析热噪声和闪烁噪声的占比¶
(1)数据预处理¶
- 为得到更加精确的数据,现将仿真参数调整如下:
图10:调整后更精细的仿真参数
- 将噪声仿真后的ZTerm的仿真数据做处理:对于每一个频率下的四个MOS器件,将其id和fn分别加起来,作为该频率下的热噪声功率谱密度和闪烁噪声功率谱密度的值。举个例子:
图11:11.4814khz下的仿真数据
如上图,该频率下的热噪声功率即为4个id相加,闪烁噪声功率即为4个fn相加。(单位:\(V^2/Hz\))
- 用python计算ZTerm的所有频率下的数据,作为对应频率下的热噪声和闪烁噪声功率谱密度。
列出部分结果如下:
| number | Frequency_(\(\(Hz\)\)) | Cumulative_ID(\(v^2/Hz\)) | Cumulative_FN(\(v^2/Hz\)) |
|---|---|---|---|
| 0 | 1.00000e+00 | 1.57418e-11 | 1.03119e-08 |
| 1 | 1.01160e+00 | 1.57418e-11 | 1.02138e-08 |
| 2 | 1.02330e+00 | 1.57418e-11 | 1.01165e-08 |
| 3 | 1.03510e+00 | 1.57418e-11 | 1.00203e-08 |
| 4 | 1.04710e+00 | 1.57418e-11 | 9.92488e-09 |
| ... | ... | ... | ... |
| 1412 | 1.14815e+07 | 5.28799e-17 | 5.65691e-20 |
| 1413 | 1.16145e+07 | 5.16196e-17 | 5.47032e-20 |
| 1414 | 1.17490e+07 | 5.03908e-17 | 5.28990e-20 |
| 1415 | 1.18850e+07 | 4.91921e-17 | 5.11571e-20 |
| 1416 | 1.20000e+07 | 4.82123e-17 | 4.97443e-20 |
表2:不同频率下的热噪声功率和闪烁噪声功率
共1417个数据。
(2)总输出热噪声的计算¶
-
将表2中得到的热噪声功率与频率的数据做拟合,并对1hz到12Mhz(0db点)做定积分积分,即可得到总输出热噪声。
-
频率与功率均取线性坐标,拟合图像如下:
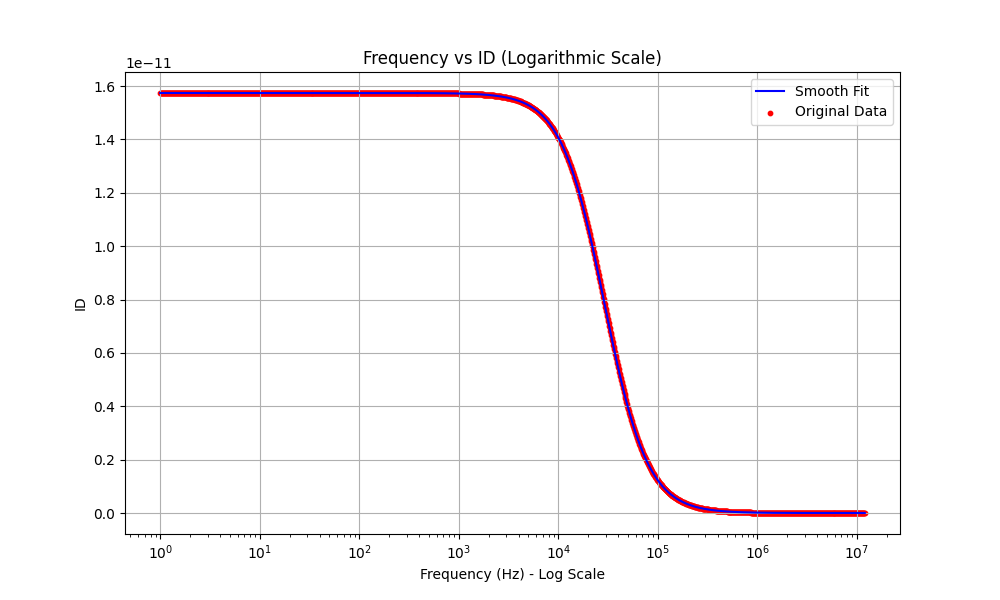
图12:线性坐标1hz-12Mhz下的热噪声功率谱
- 频率取对数坐标,拟合图像如下
图13:对数坐标1hz-12Mhz下的热噪声功率谱
- 波特图:
图14:热噪声功率谱波特图
- 对功率谱在1hz-12Mhz下求定积分,得到总输出热噪声(\(V^2\)):
(3)闪烁噪声的计算¶
-
将表2中得到的闪烁噪声功率与频率的数据做拟合,并对1hz到12Mhz(0db点)做定积分,即可得到总输出闪烁噪声。
-
频率和功率均取线性坐标,拟合图像如下:
图15:线性坐标1hz-12Mhz下的闪烁噪声功率谱
- 频率取对数坐标,拟合图像如下
图16:对数坐标1hz-12Mhz下的闪烁噪声功率谱
- 波特图:
图17:对数坐标1hz-12Mhz下的闪烁噪声功率谱
- 对功率谱在1hz-12Mhz下求定积分,得到总输出闪烁噪声(\(V^2\)):
(4)与仿真结果验证¶
- 将总输出闪烁噪声和总输出热噪声相加并开方,得到等效输出噪声。
- 结果非常Amazing啊。与图9的1.0113mV可以说是一模一样,
我怀疑aether就是这么算的
图18:之前的图9:噪声仿真
(5)热噪声与闪烁噪声对比¶
- 热噪声和闪烁噪声的波特图曲线放在一起:
图19:对数坐标1hz-12Mhz下的闪烁噪声功率谱
经过拟合得到的转折频率为3020.00 Hz
-
不难得到
-
热噪声占比:从仿真结果来看,热噪声主要在高频段显著。在优化后的OTA中,通过调整器件参数,热噪声在总体噪声中占较大比重,尤其在高于3 kHz的频率段。
闪烁噪声占比:闪烁噪声在低频段显著,其随频率增加呈指数级下降,对电路的低频信号干扰大。实验表明,在频率低于3 kHz时,闪烁噪声为主要噪声源,而在更高频率下其影响逐渐减弱。
-
在1Hz-12MHz的全频段下,总的热输出噪声功率与总的闪烁输出噪声功率之比为:
四、实验总结¶
- 优化设计与噪声性能:在OTA电路设计中,噪声性能受到晶体管宽长比、跨导增益和偏置电流等因素影响。本次实验通过增大晶体管宽长比、减少沟道长度调制效应、提升增益,成功将电路输入等效噪声降至10 μV以下。
- 热噪声和闪烁噪声的频率特性与占比:通过仿真数据处理,实验中清晰地展示了不同频段下噪声的占比特性:闪烁噪声在低频段(3 kHz以下)主导影响信号,而高频段则以热噪声为主。这一特性表明,在低频电路设计中应优先考虑闪烁噪声的抑制,尤其在音频和传感器信号处理应用中。此外,热噪声的频谱分布相对均匀,在高频段对信号影响显著,需通过提升增益与优化电流偏置予以抑制。
- Python数据处理的应用:在本实验的噪声数据分析与处理过程中,Python发挥了重要作用。通过Python对各频率下的热噪声和闪烁噪声数据进行累加、拟合及积分,生成了噪声波特图,确保噪声特性分析的精确性。最终计算出的总输出热噪声和闪烁噪声与仿真值一致,进一步验证了数据处理的准确性和效率。