电阻失配对 CMRR 的影响分析及仿真验证¶

2024.11.13

摘　要：

在模拟集成电路设计中，共模抑制比（CMRR）是运算放大器的关键性能指标。本实验通过理论分析、程序仿真和电路仿真，深入探究电阻失配对 CMRR 测试的影响。理论推导得出电阻失配会影响测试电路传递函数，进而影响 CMRR 测量值。程序仿真以设定的电阻误差模型和理论 CMRR 值，运用蒙特卡罗方法模拟不同失配误差下的影响。本实验全面研究了电阻失配对 CMRR 的影响，为模拟集成电路设计中提高 CMRR 测试准确性提供了重要参考。

实验目标¶

通过分析电阻失配对共模抑制比（CMRR）的影响，理解电阻匹配对电路性能的关键作用。
设计并使用仿真测试电路对不同失配率下的CMRR进行测量。
应用Python蒙特卡罗方法模拟电阻失配，分析CMRR的分布规律及误差容忍度。
使用仿真工具验证理论分析结果，确定失配率对CMRR测量值的具体影响程度。

实验要求¶

在“11.2.5仿真实验：5管OTA的共模抑制比CMRR设计与优化”关于CMRR仿真测试的测试台电路中，通过公式推导给出电阻失配对CMRR测试的影响，并尝试通过仿真进行验证。

Overview¶

在教材219页11.2.4仿真实验中，最终的五管OTA电路如下：

图1：五管OTA电路

测试电路如下：

图2：测试电路

仿真参数设置如下：

图3：仿真参数

测试结果如下：

图4：测试结果

可以看出，CMRR的最低值为83.37db，之后将以此为理论值进行推演。

理论求解¶

现要考虑电阻失配对测试得到CMRR的影响，由此修改电路如下：

图5：考虑电阻失配的测试电路

对N点和P点使用节点电压法，得到：

\[ \begin{align} \frac{V_{N}}{R_{1} \parallel R_{2}} &= \frac{V_{in}}{R_{1}} + \frac{V_{out} }{R_{2}}\tag{1} \\[10pt] \frac {V_P} {R_3 \parallel R_4} &= \frac {V_{in}} {R_3} \tag{2} \\ \end{align} \]

共模输入电压\(A_{CM}\)和差模输入电压\(A_{DM}\)分别为：

\[ \begin{align} V_{CM} &= \frac {V_P+V_N} {2} \tag{3} \\[10pt] V_{DM} &= V_P - V_N \tag{4} \end{align} \]

联立(1)-(4)式，得到：

\[ \begin{align} V_{CM} &= \frac {V_P + V_N} {2} \\ &= \frac{R_4} {2(R_3 + R_4)} V_{in} \ + \frac{R_2} {2(R_1 + R_2)} V_{in} \ + \frac{R_1} {2(R_1 + R_2)} V_{out} \tag{5} \\[10pt] V_{DM} &= {V_P - V_N} \\ &= \frac{R_4} {R_3 + R_4} V_{in} \ - \frac{R_2} {R_1 + R_2} V_{in} \ - \frac{R_1} {R_1 + R_2} V_{out} \tag{6} \\ \end{align} \]

由于CMRR定义为差模-差模增益\(A_{DD}\)和共模-差模增益\(A_{DC}\)的比值，同时这两个增益和运算放大器输入、输出电压的小信号关系需满足：

\[ V_{out} = V_{DM} \cdot A_{DD} + V_{CM} \cdot A_{DC} \tag{7} \]

联立(5)-(7)式，得到

\[ \begin{align} H(s)&=\frac {V_{out}} {V_{in}}\\[10pt] &=\frac{ \frac {R_4} {R_3+R_4} A_{DD} -\frac {R_2} {R_1+R_2} A_{DD} + \frac {R_4} {2( R_3 + R_4) }A_{DC} + \frac {R_2} { 2( R_1 + R_2)} A_{DC} } { 1 + \frac {R_1} { R_1 + R_2} A_{DD} - \frac {R_1} {2 ( R_1 + R_2)} A_{DC}} \tag{8} \end{align} \]

由\(\text {CMRR} =\frac { A_{DD} } { A_{DC} }\)，对(8)式子变形得到：

\[ \begin{align} H(s)=\frac{ \frac {R_4} {R_3+R_4} \text {CMRR} -\frac {R_2} {R_1+R_2} \text {CMRR} + \frac {R_4} {2( R_3 + R_4) } + \frac {R_2} { 2( R_1 + R_2)} } {\frac {1} {A_{DC}} + \frac {R_1} { R_1 + R_2} \text {CMRR} - \frac {R_1} {2 ( R_1 + R_2)} } \tag{9} \end{align} \]

观察(9)式分母，无论电阻如何失配，\(\frac {R_1} {2 ( R_1 + R_2)}\)和\(\frac {1}{A_{DC}}\)相对于\(\frac {R_1} { R_1 + R_2} \text {CMRR}\) (Overview中提到过为83.37db \(\approx\)14700)而言都要小很多数量级别，因此可以忽略，于是传递函数变为:

\[ \begin{align} H(s) =\left[ \frac{R_4 (R_1 + R_2)}{R_1 (R_3 + R_4)} - \frac{R_2}{R_1} \right]_1 + \left [ ({\frac{R_4 (R_1 + R_2)}{2 R_1 (R_3 + R_4)} + \frac{R_2}{2 R_1}})\cdot \frac{1} {\text{CMRR}_{\rm theroy}} \right]_2 \tag{10} \end{align} \]

而

\[ \text{CMRR}_{\rm measure} = ({\frac{R_2}{R_1}})_{\rm theroy} \cdot \frac{1}{H(s)} \tag {11} \]

仔细观察(10)的\(\([\ \ ]_1\)\)和\([ \ \ ]_2\)两部分，会发现后者由于\(\frac {1} {\text{CMRR}_{\rm theroy} }\)的存在会使\([\ \ ]_2\)变得极小。实际上，在不考虑失配，即四个电阻都相等时，\([\ \ ]_1\)式将为0，整个传递函数\(\(H(S)\)\)的值将由\([\ \ ]_2\)决定，这个值本就很小。因此，在考虑失配的情况下，\(H(S)\)的值将几乎完全由\([\ \ ]_1\)式决定。于是有：

\[ \begin{align} \text{CMRR}_{\rm measure} &= \left ({\frac{R_2}{R_1}} \right)_{\rm theroy} \cdot \frac{1}{H(s)}\\[10pt] &=\left(\frac {R_2} { R_1 } \right)_{\rm theroy} \cdot \frac {R_1 ( R_3 + R_4 )} { R_4 (R_1+R_2) - R_2 (R_3+R_4)} \tag{12} \end{align} \]

因此，在失配存在且达到一定程度时，\(\rm CMRR\)的测量值将完全被这些失配电阻决定。~~可怜的CMRR，被失配电阻玩弄于股掌之间~~
接下来，将从理论实验和仿真实验两个角度来验证上述结论,并探究测试电路对失配误差的容忍度(tolerance)。

理论实验¶

实验功能¶

设计一段 Python 程序，用于通过蒙特卡罗方法模拟电阻失配对电路 CMRR 的影响。具体思路如下：

1.设定电阻误差模型：假设四个电阻 \(R_1, R_2, R_3, R_4\) 的标称值为 100MΩ，并且其阻值符合千分之一（±0.1%）（这个误差值会视情况而调整）的正态分布。根据 3σ 原则，设定该分布的范围。

2.设置理论值 \(\rm CMRR_1\)：为简化运算，设定一个固定常数 \(\text{CMRR}_1 = 14000\) \(\approx\)83db作为理论 \(\rm CMRR\)参考值。

3.计算 H(s) 并进行蒙特卡罗仿真：\(H(s)\)受电阻误差影响而成为随机变量。通过蒙特卡罗方法生成 10000 份随机的电阻值，计算得到对应的 10000个 \( H(s) \)值。公式如下：

\[ \begin{align} H(s) =\left[ \frac{R_4 (R_1 + R_2)}{R_1 (R_3 + R_4)} - \frac{R_2}{R_1} \right]_1 + \left [ ({\frac{R_4 (R_1 + R_2)}{2 R_1 (R_3 + R_4)} + \frac{R_2}{2 R_1}})\cdot \frac{1} {\text{CMRR}_{\rm 1}} \right]_2 \tag{13} \end{align} \]

4.计算每次情况下的 \(\rm CMRR_2\)作为实验测量值：对于每一个\(H(s)\) ，计算 \(\text{CMRR}_2 = ({\frac{R_2}{R_1}})_{\rm theory} \cdot \frac {1}{H(s)} = \frac {1}{H(s)}\) ，作为测量值。

5.计算分贝值并绘制散点图：将每个 \(\text{CMRR}_2\) 转换成分贝值，即 \(20 \log ( \text{CMRR}_2)\)，生成 10000 个 \(\text{CMRR}_2\)和 \(20 \log(\text{CMRR}_2)\)的散点图，统计相关数据，展示结果分布。

千分之一误差仿真¶

通过设置阻值失配误差为±0.1%,跑10000个数据，得到结果如下：

图5：CMRR测量值的分布结果

由56，可以清晰看出，数据集中在60-80db这个区间（出现的负值无法显示在图5右侧，所以这个分布严格来说也是不可信的），与图4在83db附近的情况完全不同。更加有趣的是，我还统计了如下数据：

CMRR2指标	数值
低于 12000 的个数	9036
低于 12000 的比例	90.36%
为负数的个数	4190
为负数的比例	41.90%
平均值	-9467.78
标准差	655913.20
95%置信区间	（-3387.87，22323.45）
99%置信区间	（-7427.41，26362.99）

表1：±0.01%误差下CMRR2测量指标

可以看出超过90%的实验值都偏小，甚至41.5%的实验值出现了负值。该失配误差下的测量值毫无意义。

万分之一误差仿真¶

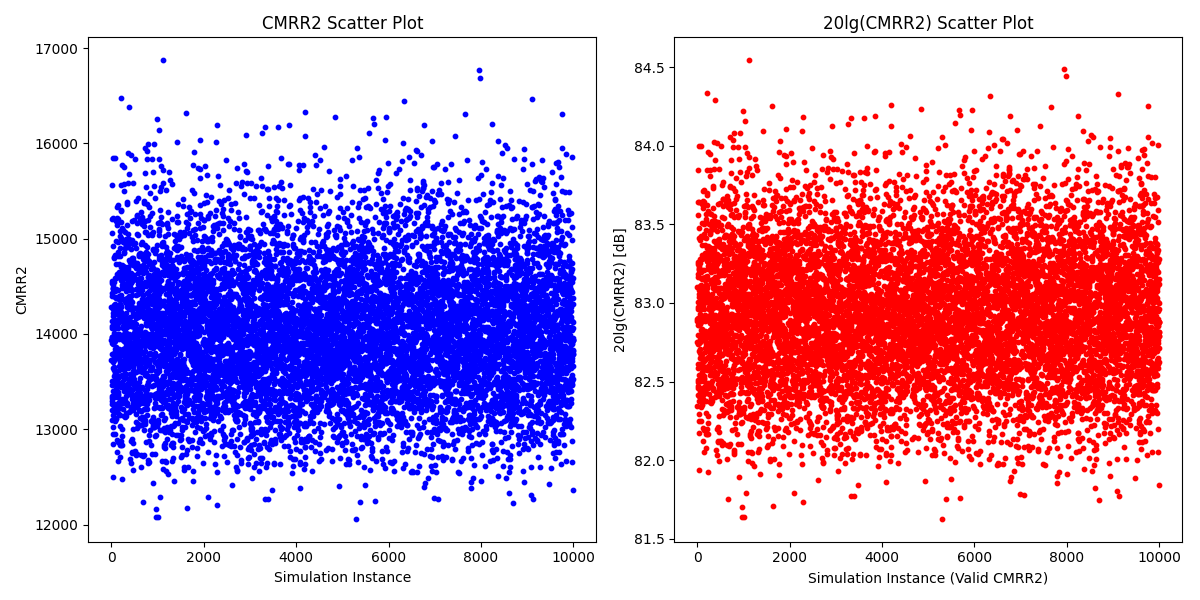
通过设置阻值失配误差为±0.01%,跑10000个数据，得到结果如下：

图6：CMRR测量值的分布结果

由图6，尤其是图6的右半部分可以清晰看出，数据在80-90db附近分布得较为集中，与图4在83db附近的情况类似，但是测量指标如下：

CMRR2指标	数值
低于 12000 的个数	3765
低于 12000 的比例	37.65%
为负数的个数	157
为负数的比例	1.57%
平均值	16759.46
标准差	241771.08
95%置信区间	（12020.84，21498.09）
99%置信区间	（10531.85，22987.08）

表2：±0.01%误差下CMRR2测量指标

可以看出超过三分之一的实验值都偏小，甚至还有1.57%的结果出现了负值，最后的平均值却大于14000的理论值。结合95%和99%置信区间，可以得出，该失配误差下，测量值已没有意义。

十万分之一误差仿真¶

通过设置阻值失配误差为±0.001%,跑10000个数据，得到结果如下：

图7：CMRR测量值的分布结果

由图7可以看出，数据在83db附近分布十分集中，与图4在83db附近的情况类似，测量指标如下：

CMRR2指标	数值
低于 12000 的个数	0
低于 12000 的比例	0
为负数的个数	0
为负数的比例	0
平均值	14027
标准差	657.42
95%置信区间	（14013.80，14040.58）
99%置信区间	（14010.76，14044.62）

表3：±0.001%误差下CMRR2测量指标

可以看出，这次的实验测量值十分集中，甚至要比图4的测量结果还要集中。通过95%和99%的置信区间得到：尽管14000的理论值没都在两个置信区间里（汗）。十万分之一，即±0.001%的失配误差下，测量值的可信度才达到要求，可用测量值来估计理论值。
可实际测试电路的电阻精度能达到±0.001%吗？

"Can be or can not be, that's the question."

电路仿真¶

千分之一误差仿真¶

考虑将图5中\(R_2\)和\(R_3\)降低0.1%为99.9M，将\(R_1\)和\(R_4\)增加0.1%为100.1M。考虑这一失配情况下的仿真结果。

图8:千分之一电阻失配

仿真结果如下：

图9：千分之一失配下的仿真结果

可以看出CMRR只在53db左右，已无实际意义。

万分之一误差仿真¶

考虑将图5中\(R_2\)和\(R_3\)降低0.01%为99.99M，将\(R_1\)和\(R_4\)增加0.01%为100.01M。考虑这一失配情况下的仿真结果。

图10:万分之一电阻失配

仿真结果如下：

图11：万分之一失配下的仿真结果

可以看出CMRR只在73db左右。6.33k，降了一倍多，依然是没有实际意义，参考价值不大。

十万分之一误差仿真¶

考虑将图5中\(R_2\)和\(R_3\)降低0.001%为99.999M，将\(R_1\)和\(R_4\)增加0.001%为100.001M。考虑这一失配情况下的仿真结果。

图12:十万分之一电阻失配

仿真结果如下：

图13：十万分之一失配下的仿真结果

虽然这次数据的集中度明显偏好，但是和图4对比，结果明显偏大，依然不可信。
电路仿真结果与程序仿真结果出现出入，可能的原因如下：
程序中电阻的±0.001%失配是以此为边界，按照3σ原则的正态分布，实际能直接取到的边界值的情况站10000个数据的比例并不大，而电路仿真则是直接取了一个极限的边界值来研究问题。
即便不考虑失配，83db在图4中也是最低值，并且图4的测试值也并不集中，而是十分分散。在程序中为了简便直接取83db=14000作为理论值，并未考虑CMRR理论值的浮动情况。
因此在程序中，±0.001%的精度表现出良好的收敛特性。而在电路仿真中，±0.001%的精度依然让测试结果不可信。

实验总结¶

理论分析成果：运用节点电压法对包含电阻失配的测试电路进行分析，成功推导出电阻失配影响 CMRR 测试的理论公式，清晰地揭示了电阻失配与 CMRR 之间的内在关系。
程序仿真结论：设计的 Python 程序有效地模拟了不同电阻失配误差下电路 CMRR 的变化情况。
在 ±0.1% 的失配误差下，超过 90% 的实验值偏小，甚至 41.90% 为负值，测量值毫无意义；
±0.01% 的失配误差下，超过三分之一实验值偏小，1.57% 为负值，平均值虽大于理论值，但测量值已不可信；
而在 ±0.001% 的失配误差下，实验测量值集中在理论值附近，可信度较高，从而确定了在程序模拟中较为合理的电阻失配范围。
电路仿真发现：实际电路仿真中，设置千分之一、万分之一和十万分之一的电阻失配情况，结果表明失配均导致 CMRR 值偏离理论值。千分之一失配时 CMRR 在 53db 左右，万分之一失配时约为 73db，十万分之一失配时虽数据集中度较好但与理论值对比明显偏大。同时，电路仿真结果与程序仿真结果存在差异，原因在于程序中电阻失配按正态分布取值，实际能取到边界值比例小，而电路仿真直接取极限边界值，且程序为简便采用固定理论值未考虑实际浮动。
综合实验意义：本实验全面深入地探究了电阻失配对 CMRR 测试的影响，为模拟集成电路设计中准确测试 CMRR 提供了重要参考。